Last year I happened to play this game called Aces & Adventures (2023), which seems like it was modestly successful but I haven’t seen anyone else mention or talk about. I enjoyed it quite a bit! It’s a deckbuilding RPG, with various classes, and each campaign has you playing through a node graph of combat challenges. Slay the Spire (2019) casts a long shadow, but A&A is pretty unlike most of the usual derivatives. Most notably, it uses traditional card ranks and suits, and you attack by making Poker hands. That’s a relatively uncommon premise (or it was), and for that reason it’s really interesting to compare and contrast to the uber-successful Balatro (2024) which came out a year later. A&A has some design issues (or at least a design direction I don’t really understand), but the core combat mechanic is good and fun, for many of the same reasons Balatro’s is. You’re playing with familiar cards and making hands like in Poker, but unlike with real cards, you have a whole bunch of deck manipulation mechanics and various kinds of wild cards which help smooth out the randomness. It’s good!

But I wanted to mention a rabbit hole it pulled me down, which was trying to figure out Poker-like probabilities in nonstandard situations. Poker hand probabilities are well studied for obvious reasons, but in a relatively static and brittle way. If you want to know the probability of any given card hand, it isn’t difficult to find the answer, as long as you only care about situations using a traditional deck and with a 5 or 7 card hand used by most all Poker variants (five since that’s what a “hand” consists of, and seven since you often are trying to make a five card hand out of seven possible cards). But I’m a game designer! I care about many more types of card situations than just those that already exist.
In A&A (as in Balatro), you’re often drawing many more cards than normal. But unlike in Balatro, here you’re making hands competitively against a computer opponent who’s doing the same. Simplifying it a bit, essentially the mechanic works like this:
- You draw some number of cards.
- You make the best ‘hand’ you can of N cards.
- But only counting the “load-bearing” part of a hand! As in, “Three of a kind” is just the three matching cards, you don’t play the two unmatched cards. Or if you play an Ace as a high card, it’s just that single Ace by itself. So there’s never a kicker, which actually changes things quite a bit.
- Then, the computer then draws a bunch of cards (the number is determined by an attack/defense calculation) from its own separate deck, and then it tries to make the best N-card hand it can to play against yours.
- A nuance to the above to consider is that the computer can’t play a hand with more cards than you played. So if I attack with two 8s, and the computer draws four 7s, the best it can do is play two 7s and lose. Which must be pretty frustrating for it I guess.
All in all, this is actually pretty far from normal Poker math, even ignoring that we’re dealing from two separate decks too.
Given the above, attacks fall neatly into only a few categories: We can make hands that are 1 card (a single high card), 2 cards (pairs), 3 cards (three-of-kinds), 4 cards (four-of-a-kinds and two-pairs) or 5 cards (straights, flushes, full houses). And… that’s it, those are all of the valid attacks we can make.
So then what we want to know is, given the hand we play, what are the odds the computer will draw a better set of cards? I mean like this: Say I play a three-of-a-kind of 10s, then the opponent draws 8 cards. What’s the probability they’ll draw a higher ranked three-of-a-kind from within those eight cards?
I found this was far enough off of the beaten trail of Poker math that I couldn’t find any answers about it (although Durango Bill’s that I linked to above covers a lot that’s close). So, I tried to derive it all myself.
And the result of that was I decided to write a Steam guide about it!
You can check it out here: Win % Odds for Cards in Attacks
It really makes me laugh, because it’s pretty far removed from actually being tactically useful gameplay information. I really just wrote it as a way to externalize the work I put in on the math problem, it really should be more of a blog post than a Steam guide. And ironically, here I am writing about a blog post about the guide.
But in answering this probability question, I found there was some interesting nuance in the answers! I would not have guessed the distribution on the 1 card odds:
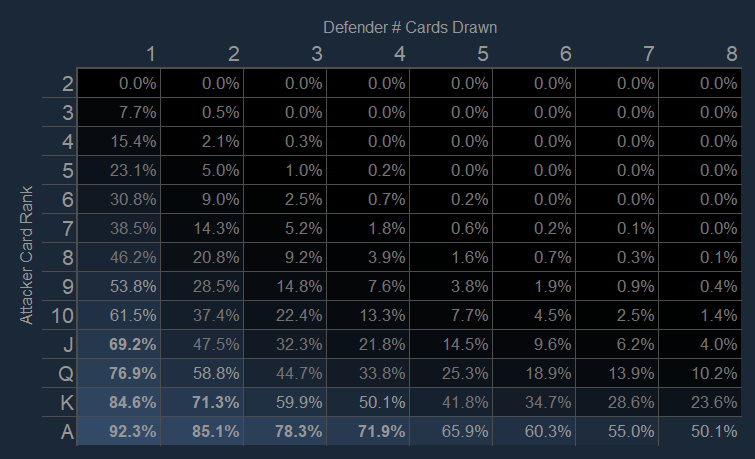
Intuitively, if I attack with a 10, and the opponent draws eight cards, it makes sense the odds are pretty stacked against me. But I’m surprised at the steep drop-off from Ace to King to Queen. That your probability with an Ace against eight cards is better than a Jack against two cards, for example, seems somewhat surprising to me. There’s more like that in the guide, even if none of it really matters too much in terms of strategy.
Arbitrary Cards
Anyway you can read the guide if you like. But I’m still wondering about the underlying problem I was thinking about.
What I really want is this:
Given a deck of arbitrary specifications (i.e., an arbitrary/nonstandard number of ranks and suits), what is the probability of a given type of hand, when dealt a hand of X cards?
But as far as I can tell, there’s no general solution to figuring that out, besides doing all the combinatorial math yourself, or brute-force Monte Carlo-ing the calculation. Which is too bad, I guess I’ll never get to play interplanar multiverse Poker.
Leave a Reply